Case 3 Help: Tunnel with an Airshaft
Case 3 simulates pressures and velocities when a train travels through a tunnel with an airsfhaft. In older tunnels, airshafts were often built to provide additional tunnel faces during construction and were retained for ventilation purposes. In modern tunnels, they are more likely to be provided for the express purpose of reducing potential discomfort to passengers from pressure waves generated during train-entry and train-exit.
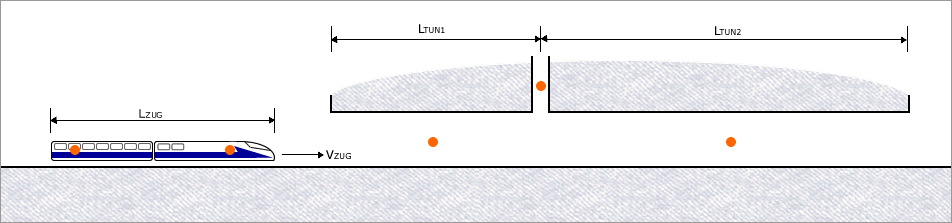
 Location of pressure and/or
velocity output
Location of pressure and/or
velocity output Output Locations
The principal use of Case-3 simulations is expected to be the prediction of pressures experienced by passengers on trains. However, some output is also provided at selected tunnel locations.
Graphical output is provided as follows:
Box-1: Pressure histories in the tunnel
(1) at the middle of Tun-1 (upstream of the airshaft)
(2) at the middle of Tun-2 (downstream of the airshaft)
Box-2: Pressure histories inside the front and rear coaches
of the train
Solid lines - outside the train
Broken lines - inside the train
NB: For unsealed trains, there is little difference between pressures
inside and outside coaches. For well-sealed trains, sufficiently rapid external
pressure changes are strongly damped. Large values of the sealing time constant
correspond to tight seals and small values correspond to poor seals.
Box-3: Mean air velocity histories in the tunnel
(1) at the middle of Tun-1 (upstream of the airshaft)
(2) at the middle of Tun-2 (downstream of the airshaft)
(3) at the middle of the air shaft
Box-4: Train speed
Text output is provided in the V01.txt file as follows:
- Pressure and mean-velocity histories at
(1) at the middle of Tun-1 (upstream of the airshaft)
(2) at the middle of Tun-2 (downstream of the airshaft) - Mean-velocity history in the middle of the air shaft
- Pressure histories inside the front and rear coaches of the train
(1) for an unsealed train
(2) for a sealed train with a time constant of 10 s - Train speed history
LTUN1, m: Distance between entrance portal and shaft
For most purposes, the meanings of distances between locations in the tunnel is self-evident. If you want to be more precise, give the distance between (i) the centroid of the portal cross-section and (ii) the centroid of the shaft cross-section at its junction with the tunnel. This is not a formal definition, but it is probably good enough.
In ThermoTun-Online, the distance between the entrance portal and the shaft must be at least 200m. The full version of ThermoTun allows experienced users to choose any length greater than zero. ThermoTun-Online is intended only for applications in which one-dimensional analyses can be used with reasonable confidence.
LTUN2, m: Distance between shaft and exit portal
For most purposes, the meanings of distances between locations in the tunnel is self-evident. If you want to be more precise, give the distance between (i) the centroid of the shaft cross-section at its junction with the tunnel and (ii) the centroid of the portal cross-section. This is not a formal definition, but it is probably good enough.
In ThermoTun-Online, the distance between the shaft and the entrance portal must be at least 200m. The full version of ThermoTun allows experienced users to choose any length greater than zero. ThermoTun-Online is intended only for applications in which one-dimensional analyses can be used with reasonable confidence.
ATUN, m2: Cross-sectional area of tunnel
For most purposes, the meaning of the cross-sectional area of the tunnel is self-evident. If you want to be more precise, calculate the total volume of air in the tunnel and divide this by the total tunnel length. This is not a formal definition, but it is probably good enough.
In ThermoTun-Online, the area of the tunnel must be at least 10m2. The full version of ThermoTun allows experienced users to choose any area greater than zero. ThermoTun-Online is intended only for conventional train:tunnel applications.
With large cross-sectional areas, the assumptions of one-dimensional flow can become suspect. It is recommended that the effective diameter of the tunnel should not exceed 10-20% of the length of any region of tunnel between boundaries. (NB: The “effective diameter” is the diameter of a circle with the same cross-sectional area as the tunnel).
FTUN (f): Tunnel friction coefficient (Fanning, not Darcy-Weisbach)
The tunnel skin friction coefficient determines the resistance to airflows along the tunnel. There are two definitions in common use:
Fanning (f ): Wall shear stress = f x ρU 2/2
Darcy-Weisbach (λ ): Wall shear stress = λ x ρU 2/8
where ρ is the density of the air and U is the mean velocity along the tunnel.
It follows from the definitions that λ=4f so it is important to know which one is used in any particular software. ThermoTun uses f, not λ.
The Fanning friction coefficient for real tunnels will exceed 0.002. It will usually be within the range 0.005 < f < 0.010.
DXW0, m: Numerical grid length
Values of pressure and velocity are calculated at closely spaced points throughout the tunnel system. The distance between adjacent calculation points (i.e. the numerical grid length) is either 0.25% of the total length of the tunnel or 20% of the train length (whichever is smaller). The full version of ThermoTun allows experienced users to choose any grid length greater than zero,
LSHA, m: Length of shaft
For most purposes, the meanings of distances between locations in the tunnel system is self-evident. If you want to be more precise, give the distance along the shaft axis between (i) the centroid of its portal cross-section and (ii) the centroid of the tunnel cross-section at its junction with the shaft. This is not a formal definition, but it is probably good enough.
For numerical accuracy, the length of the shaft must be at least one grid length and preferably at least 2 grid lengths. . The full version of ThermoTun allows experienced users to choose any length greater than zero. ThermoTun-Online is intended only for applications in which one-dimensional analyses can be used with reasonable confidence.
ASHA, m2: Cross-sectional area of shaft
For most purposes, the meaning of the cross-sectional area of the shaft is self-evident. If you want to be more precise, calculate the total volume of air in the shaft and divide this by the shaft length. This is not a formal definition, but it is probably good enough.
In ThermoTun-Online, the area of the shaft must be at least 2% of the area of the tunnel. The full version of ThermoTun allows experienced users to choose any area greater than zero. ThermoTun-Online is intended only for conventional train:tunnel applications.
KINSHA: Loss coefficient, inflow to tunnel through shaft
Because shafts are usually quite short, the resistance to flow along them is often influenced more strongly by end conditions that by friction on their internal surfaces. ThermoTun-Online assumes that the overall resistance to inflow through the shaft is equivalent to a stagnation pressure loss of KINSHA x ρU 2/2 . The full version of ThermoTun allows experienced users to specify local losses at the ends of shafts and skin fiction along them.
The prescribed values of the shaft loss coefficients must be in the range 0 to 5. This range is sufficient for conventional shafts. The full version of ThermoTun allows experienced users to choose any value greater than zero.
KOUTSHA: Loss coefficient, outflow from tunnel through shaft
Because shafts are usually quite short, the resistance to flow along them is often influenced more strongly by end conditions that by friction on their internal surfaces. ThermoTun-Online assumes that the overall resistance to outflow through the shaft is equivalent to a stagnation pressure loss of KOUTSHA x ρU 2/2 . The full version of ThermoTun allows experienced users to specify local losses at the ends of shafts and skin fiction along them.
The prescribed values of the shaft loss coefficients must be in the range 0 to 5. This range is sufficient for conventional shafts. The full version of ThermoTun allows experienced users to choose any value greater than zero.
LZUG, m: Length of train
For most purposes, the meaning of train length is self-evident. If you want to be more precise and the train ends are strongly tapered, give the distance between the most extreme points. This is not a formal definition, but it is simple and it is probably good enough. The full version of ThermoTun allows experienced users to simulate trains comprising multiple coaches, each with any length greater than zero.
The prescribed length of the train must be at least 50m. The full version of ThermoTun allows experienced users to simulate trains comprising multiple coaches, each with any length greater than zero. ThermoTun-Online is intended only for applications in which one-dimensional analyses can be used with reasonable confidence. In reality, phenomena such as nose-entry and tail-entry to a tunnel exhibit three-dimensional behaviour that extends the period of development of pressure changes.
It is recommended that the train length should be equivalent to at least 10 tunnel diameters. This is because ThermoTun-Online is intended only for applications in which one-dimensional analyses can be used with reasonable confidence. The full version of ThermoTun allows experienced users to simulate trains comprising multiple coaches, each with any length greater than zero.
For numerical accuracy, it is preferable for the train length to be at least 1% of the total tunnel length. This is because the numerical grid length used in ThermoTun-online is approximately ½% of the tunnel length. The full version of ThermoTun allows experienced users to vary the numerical grid size within wide limits.
AZUG, m2: Cross-sectional area of train
For many purposes, the meaning of the cross-sectional area of a train is self-evident. For the calculation of airflows in tunnels, a rather special meaning is implied (irrespective of which software you use). The key need is to simulate the blockage effect of the train. For a passenger coach, for example, the effective aerodynamic area is bigger than the cross-section of the passenger compartment, but smaller than the overall structural envelope including the underbody and bogies, etc.
The area of the train must be at least 5m2 and the blockage ratio in the tunnel must not exceed 50%. The full version of ThermoTun allows experienced users to choose any area greater than zero. ThermoTun-Online is intended only for conventional train:tunnel applications.
FZUG (f) Train friction coefficient (Fanning, not Darcy-Weisbach)
The train skin friction coefficient determines the main component of resistance to airflows in the annulus between the sides of the train and the tunnel. There are two definitions in common use:
Fanning (f ): Wall shear stress = f x ρU 2/2
Darcy-Weisbach (λ ): Wall shear stress = λ x ρU 2/8
where ρ is the density of the air and U is the mean velocity (relative to the train in this instance).
It follows from the definitions that λ=4f so it is important to know which one is used in any particular software. ThermoTun uses f, not λ.
If you have no experience of estimating train friction coefficients, the following values are indicative of some typical trains (but only indicative):
• modern streamlined passenger train: f ≈ 0.003
• conventional regional passenger train: f ≈ 0.005
• container-like freight train: f ≈ 0.007
The Fanning friction coefficient for real trains will exceed 0.002. It will usually be within the range 0.003 < f < 0.010.
KNOSE: Loss coefficient, flow from open tunnel into annulus around train
In addition to skin friction on train and tunnel surfaces in the annulus around a train, account is usually taken of local losses at the nose and tail. These influence the amplitudes of pressure waves as well as the overall resistance to flow. When the direction of airflow relative to the train is from the open tunnel into the annulus, ThermoTun allows for a stagnation pressure loss given by KNOSE x ρU 2/2, where ρ denotes the air density and U is the air velocity relative to the train in the annulus.
The prescribed value of the nose loss coefficient must be in the range 0 to 0.5. This range is sufficient for all conventional trains. The full version of ThermoTun allows experienced users to choose any value greater than zero.
STAIL: Shape factor, flow from annulus around train into open tunnel
When the direction of airflow relative to the train is from the annulus into the open tunnel, ThermoTun allows for a stagnation pressure loss given by KTAIL x ρU 2/2, where ρ denotes the air density and U is the air velocity relative to the train in the annulus. The most suitable value of KTAIL varies strongly with the train:tunnel blockage ratio. Instead of asking users to prescribe different values for each tunnel area, ThermoTun calculates the expected loss for a blunt-ended train and uses a shape coefficient STAIL to define the actual loss as: STAIL x KBLUNT x ρU 2/2.
The prescribed values of the tail shape coefficients must be in the range 0 to 1. This range is sufficient for conventional trains. The full version of ThermoTun allows experienced users to choose any value greater than zero.
TSEAL, s: Sealing time constants for leakage through coach bodies
ThermoTun calculates pressures inside trains as a consequence of leakage of air through coach bodies.
Railways commonly use a sealing time constant to characterise the leakage characteristics of coaches. Typically, a test is undertaken in which the pressure inside a coach is held at a constant value for a period and is then allowed to decay freely.
The sealing time constant is usually defined as the time required for the pressure difference to reduce to (1/e) times the original value (where e = 2.718 is the base of natural logarithms. Beware: the sealing time constant is usually determined in a static test; the corresponding value for a coach in motion can be considerably smaller. Also, it is possible for different values to exist for positive and negative pressure differences between the inside and outside of a coach.
VZUG, km/h: Speed of train
In ThermoTun-Online, the train speed is constant and is defined in km/h. The full version of ThermoTun allows accelerating, decelerating, stopping, starting and reversing. It also allows speeds to be defined in other units if required.
The prescribed value of the train speed must be in the range 50 to 400 km/h. This range is sufficient for most practical purposes.
