Case 6 Help: Micro-pressure waves (MPWs) – "sonic booms"
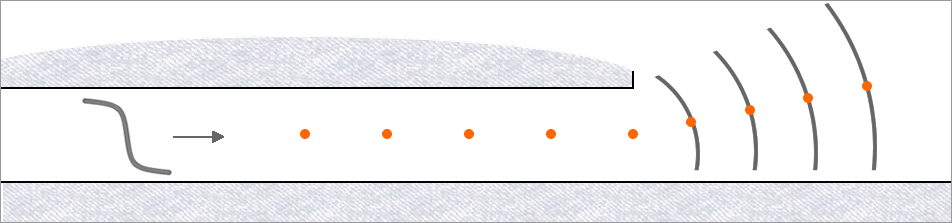
 Location of pressure output
Location of pressure outputAbout Case 6
Case 6 simulates pressure disturbances in the external environment beyond a tunnel portal when an internal wavefront arrives from upstream and reflects back along the tunnel. In most simulations with 1-D software, it is usual to assume that the pressure at a portal is approximately equal to the local atmospheric pressure at all times. In such simulations, allowance might be made for local losses applicable in steady flow, but no allowance is made for other causes of pressure change. This approximation is usually adequate for predictions of pressure fluctuations inside tunnels - even during periods of rapid change such as wavefront reflection. Nevertheless, in reality, the reflection process involves interactions between the internal and external flow-fields and a small amount of energy escapes from the tunnel, causing small, but rapid, pressure changes beyond the portal. This happens at all tunnel portals, but the effects are usually too small to worry about. In a few cases, however - notably when high-speed trains travel through long, slab-track tunnels with few, if any, shafts or other connections - the external changes can cause annoying low-frequency disturbances such as the rattling of doors and windows. Sufficiently strong wavefronts can even cause loud audible disturbances - although designers would have failed in their professional duty if this were allowed to occur today. The external disturbances are collectively known as micro-pressure waves (MPWs) and the audible components are often referred to as sonic booms.
The maximum amplitudes of the external pressure fluctuations depend primarily upon the maximum sustained rates of change of mass flow through the portal and, for simple tunnel exit regions, these are proportional to the maximum sustained rates of change of pressure in the wavefronts that induce the disturbances. This is important for practical engineering because it is relatively easy to measure pressure changes in tunnels, but almost impossible to measure mass flow rates accurately. For ThermoTun-Online, users therefore prescribe pressure histories even though the software itself uses these to deduce mass flow rates.
The user-prescribed pressure history is applied at a suitable distance upstream of the portal and the corresponding mass flow rate at that location is deduced on the assumption that the pressure change is caused exclusively by a wavefront propagating towards the portal. Users are responsible for providing pressure histories that satisfy this assumption. ThermoTun is responsible for deducing the consequences downstream, both inside and outside the tunnel.
The environment outside a tunnel portal is 3-D in nature so it cannot be
analysed using the same methods as those used to simulate wave propagation
inside tunnels. However, it would rarely be sensible to resort to fully 3-D
methods of the whole train:tunnel phenomenon simply to enable the external
disturbances to be simulated. Instead, the most common approach is to use
1-D methods to deduce the rates of change of mass flow and then to use simple
analytical expressions from the world of acoustics to estimate the consequential
disturbances. This is good enough for most practical design purposes, but
it nevertheless has theoretical limitations. Two of these are:
(1) the most commonly used analytical method is not valid close to the portal
although it is a good approximation at distances greater than a few tunnel
diameters
(2) the sequential solution is not interactive - and so the simulation of
the internal flows remains wholly independent of any external influences.
Case 6 uses an interactive solution process that enables the internal and external flowfields to influence each other. Sufficiently far from the portal, its predictions do not differ significantly from those obtained with the usual simple, non-interactive methodology. Close to the portal, however, the uncoupled method is unsatisfactory. ThermoTun provides better accuracy in this region and, in addition, it enables consequential delays on the internal reflection processes to be evaluated.
Wavefront shapes
The wavefront approaching the portal in Case-6 in ThermoTun-Online is NOT calculated ab initio by ThermoTun. Instead, it is prescribed by users, thereby enabling attention to focus on the reflection/transmission phenomenon regardless of the causes of the approaching wavefront.
• In demo mode simulations, users may choose either (a) an incident wavefront with a sinusoidal shape or (b) an incident wavefront of the form: Δp/Δpmax = (2/π)tan-1{t}, where Δp = pressure increase and t = time. In both cases, the pressure increases from zero to a maximum in a gradual manner. The rate of change of pressure increases from zero to a maximum and then reduces to zero. The second of these shapes is broadly indicative of train-induced wavefronts in real tunnels and the predicted MPWs are of practical interest. In contrast, the sinusoidal ramp is of more academic interest. Its primary purpose in the demo mode is to provide a comparison with the tan-1 example, thereby illustrating a strong dependence of the MPW on the wavefront shape as well as on its amplitude and steepness.
The tan-1 wavefront shape has the form Δp/Δpmax = 1/2 + (2/π)tan-1{t/T}, where T satisfies (∂p/∂t)max= Δpmax/T. The leading part of this form is asymptotic to Δp = 0 and the trailing part is asymptotic to Δp = Δpmax. To avoid discontinuities at the beginning and end of the pressure history, the outer (i.e. asymptotic) portions of the wavefront are replaced by quadratic forms that have zero rate of change of pressure at the beginning and end of the simulated region. This is done only in regions where the rates of change associated with the tan-1 form are less that 0.01(∂p/∂t)maxso have negligible influence on the overall predictions.
• For professional simulations, users prescribe the wavefront Δp{t}explicitly. This enables the exploration of real wavefronts, perhaps using data from full-scale measurements. Alternatively, the professional mode can be used to investigate idealised wave shapes that differ from those available in the demo mode.
* Warning *
There is an important reason for requiring users to prescribe Δp{t}
histories instead of calculating them using ThermoTun itself. This is that,
although ThermoTun can often estimate pressure amplitudes with remarkable
accuracy, neither it nor any other 1-D numerical software can make accurate
predictions of rates of change of pressure caused by trains in tunnels. This
is because the key events that cause wavefronts that give rise to MPWs - e.g.
nose x portal or nose x shaft - are fundamentally 3 D in nature. Accordingly,
it would be misleading to construct the Case 6 simulations in a manner that
gives the impression that ThermoTun predicts rates of change of internal pressure
waves accurately. It can do so in certain circumstances, but it cannot do
so in general.
ΔpMAX, kPa: Maximum pressure in the incident wavefront
In DEMO mode, the pressure in the prescribed incident wavefronts increases from zero to a maximum. Ahead of the wavefront, Δp = 0 so p = patm. Behind it, Δp = Δpmax so p = patm + Δpmax. The range of values of Δpmax available in DEMO mode covers the range that is to be expected in typical high speed railways.
(∂p/∂t)MAX, kPa/s: Maximum rate of change of pressure in the incident wavefront
Physically, the amplitudes of MPWs usually depend much more strongly on rates of change of pressure in incident wavefronts than upon the maximum pressures. Strictly, this statement applies only when the rate of change is sustained for a small interval. However, this interval is so small - typically approximately equal to the time taken for a sound wave to travel a distance equal to the tunnel diameter - that this proviso is rarely stated explicitly.
In DEMO mode, the range of values of (∂p/∂t)maxcovers the range that is of greatest interest in most practical cases. However, some combinations of Δpmax and (∂p/∂t)maxare excluded to avoid a need for excessively large simulation times.
ATUN, m2: Cross-sectional area of tunnel
For most purposes, the meaning of the cross-sectional area of the tunnel is self-evident. If you want to be more precise, calculate the total volume of air in the tunnel and divide this by the total tunnel length. This is not a formal definition, but it is probably good enough.
The area of the tunnel must be in the range 10m2 - 80m2. The full version of ThermoTun allows experienced users to choose any area greater than zero. ThermoTun-Online is intended only for conventional train:tunnel applications.
In Case-6, the software calculates the radius of a circle with the same cross-sectional area as the tunnel. It uses this to determine the location of output outside the portal.
Solid angle, steradians
The strengths of MPWs emitted from a tunnel depend upon the geometrical constraint imposed by the topography outside the portal. In ThermoTun-Online, this is characterised by a solid angle which, of necessity lies in the range 0 < Ω < 4π. The maximum value (4π) corresponds to a point source in an unrestricted space so it is irrelevant to tunnel applications. A value of 2π would apply for an infinite hemisphere so even that is unlikely. In many real cases, the most suitable value will be in the range π ± 50%.
Numerical accuracy and execution time
The accuracy of the calculations depends upon the numerical grid size. Users choose a grid size by specifying a parameter "Accuracy" that is denoted here as "Acc". It is used to choose the grid length as a proportion of the tunnel radius - i.e. Δx=RTUN/Acc. The greater the value of "Acc", the better the accuracy of the calculations, so large values should be used when acceptable to the user. However, there is an important downside, namly that the execution time varies approximately with the square of "Acc". It is recommended that users first try Acc=8 and then explore the consequences of smaller or larger values. Even the coarsest grid length used in Case 6 simulations is far smaller than that used in Cases 1 5 - and this is evident in the execution times that are required.
The execution time also depends strongly upon the length of the wavefront because this determines the length of tunnel that must be simulated upstream of the portal. However, long wavefronts tend to imply smaller rates of change of pressure so it will often be acceptable to use coarser grid lengths when simulating long wavefronts. This is always the case in the DEMO-mode examples. It will not necessarily be so in the Professional mode, however, because users are responsible for choosing the length of pressure history that is simulated. It is recommended that users should curtail their pressure histories so that the primary focus is on the most important part of the wavefront. As a rough guide, the minimum overall duration of the user-prescribed pressure history should be at least ten times greater than the minimum time taken for the pressure to increase by half of its overall range - although this guideline applies only to wavefronts increasing fairly smoothly over their whole duration.
Case 6 can take much longer to run than other cases in ThermoTun-Online and, as a consequence, it can be time limited by the web server, which will time out after 300 seconds.
ThermoTun-Online will reject any data that cause the predicted run time to exceed 300 seconds. There is no equivalent limitation in the desktop based full version of ThermoTun. In DEMO mode, the website ensures that the region of strongest pressure change is a significant proportion of the overall wavefront - i.e. the outer regions of gentle change are relatively short. This minimises wasted simulation time. In Professional mode, the user chooses the incident wavefront and is advised to curtail the data so that it does not have long outer regions of unimportant pressure change.
Output Locations
The locations at which pressure histories are output are determined by the data selected by the user.
Inside the tunnel, greatest interest is on the incident wavefront approaching the portal and reflecting back along the tunnel. The output locations are at distances of Lwave/8, 2Lwave/8, 3Lwave/8 and 4Lwave/8 from the portal plane. Here, Lwave denotes the length of the wavefront; it is the product of the wavefront duration and the speed of sound (deemed to be 340 m/s).
Outside the tunnel, greatest interest is on the rate of decay with increasing distance from the portal. Accordingly, the output locations are at Rtun, 2Rtun, 3Rtun and 4Rtun beyond the portal, regardless of the length of the wavefront.
In addition, both the static pressure and the stagnation pressure are output at the exit portal.
Finally, the user-specified pressure history is output, scaled to match the coordinate system that applies to all output.
The origin of the time coordinate used for output is the instant when the
mid length of the wavefront reaches the exit portal.
File Uploads
In PROFESSIONAL mode, users may provide their own prescribed wavefront in a tabular format. The actual origin of the prescribed wavefront is not important here. It might be, for instance, a measured pressure history in a real tunnel or an idealised history obtained from an independent analysis.
Users provide the history in a simple file containing two columns of data, namely time and pressure respectively. Thus:
t1,Δp1
t2,Δp2
t3,Δp3
etc
in which the units of time and pressure change are seconds and kiloPascals respectively (see details delow).
It is recommended that the overall time period covered in the data is as short as reasonably practicable. There is little point in calculating and outputting values in regions where the rates of change are very much smaller than the maximum value. This would waste simulation time and it would cause the region of maximum interest to be compressed into an unnecessarily small part of the output graphs.
The time coordinate listed in the tabulated and graphical output is offset from the values listed in the user-supplied data. There are several reasons for this, including:
• it relieves users of the responsibility for ensuring that the first data item is at the origin of the provided data. As a consequence, users are free to top and tail their data freely in successive simulations
• it assists in the comparison of results from simulations with different incident wavefronts. In all cases, the instant "t = 0" in the output from ThermoTun Case 6 simulations corresponds to the time when the mid-time position on the wavefront chosen reaches the tunnel portal. Suppose, for example, that the times listed in the first and last rows of the user input table are 21.6 s and 23.2 s. In this case, the mid-time point is 22.4 s. The wavefront travels along the tunnel at approximately the speed of sound and arrives at the portal at some time that is not known a priori by the user. The designation of this instant as t=0 in all output therefore eliminates the need for unnecessary calculations by the user.
Similarly, the pressure coordinate listed in the tabulated and graphical output is offset from the values listed in the user-supplied data. All pressures are expressed relative to the value listed in row-1 (which therefore corresponds to Δp=0). This avoids the possibility of a discontinuity at the beginning of the data. Users remain responsible, however, for avoiding discontinuities in the remainder of their data. Failure to do this will cause ThermoTun to detect excessively large rates of change of pressure and hence to predict unreasonably large MPWs.
For Case 6 ThermoTun-Online places restrictions on uploaded files in order to avoid data entry errors when the files are sent to ThermoTun
- The uploaded file must be in comma separated variable format with a .csv extension. Most spreadsheets can save data in this format.
- The first column must be time in seconds (s).
- The second column must be pressure in kPa.
- The .csv file must only contain numbers. Files containing any text will be rejected.
- There must be no empty rows in the .csv file.
- The time in each row should be greater than the time in the previous row.
ThermoTun Online will create error messages if the file is not in a suitable format and will ask you to alter the file and upload it again.
For examples of valid .csv input files see Case6_waveform1.csv and Case6_waveform2.csv
As indicated above, MPWs are strongly sensitive to the shape of the incident wavefront. As a consequence, it is of fundamental importance that the shape is expressed adequately in user-prescribed input. It is strongly recommended that there are at least 20 data points over the steepest region of the wavefront and that the greatest pressure change between successive data points is not more than 10% of the overall pressure change.
